IoSR Blog : 16 December 2013
Computational Auditory Scene Analysis, part 2
Time–Frequency Masking: Binary OR NOT?
In my last blog post I introduced the concept of time–frequency masking. This is a popular and powerful method of separating concurrent sounds, provided that we know which parts to change. By the way, when I say "parts" I'm referring to the pixels in the diagrams in my last blog, although these should more correctly be referred to as "time–frequency units". Research in this area generally falls in to two camps: coming up with better methods of figuring out which time–frequency units to change, and improving the separation method under the assumption that we know precisely which time–frequency units to change. Research at the IoSR covered both camps, but for the purposes of this blog post I'm going to assume that we know precisely which time–frequency units to change. This is possible because I'm going to make the mixtures myself, and so I know what all of its constituent sounds are. I'm making the optimisitic assumption that one day we will be able to figure out precisely which time–frequency units to change without this prior knowledge.
If we know which time–frequency units to change, how do we change them to get the best result? In my last post I described turning them on and off using a "binary" mask (where units in the time–frequency mask were set to 1 or 0). This is a pretty good way of going about things. If you listened to the examples you will have heard that one of the sound sources was almost completely removed. However, you may also have heard some artefacts of this process: a kind of unpleasant bubbly sound. This is a real problem. One experiment [1] found that these artefacts are so annoying, that despite the target speech becoming more intelligible, listeners prefer the unprocessed mixture. If a broadcaster wanted to use sound source separation to remove unwanted noises from a recording then this method might end up making things sound worse!
The bubbly artefacts you hear are likely to be caused by the binary mask transitioning frequently between loud (1) and quiet (0) and vice versa. So what about setting the values to between 0 and 1? Presumably this would reduce the size of these transitions, and hopefully reduce the level of the bubbly artefacts. A number of authors have suggested using such a "continuous" or "ratio" mask (you'll see why it's called a "ratio" mask shortly), and the debate is currently a hot topic in some sections of the signal processing community.
An example of binary and ratio masks are shown in the top two panels of Fig. 1. The bottom panel shows a single row from the top two plots. The large and sharp transitions of the binary mask are contrasted heavily by the softer transitions of the ratio mask.
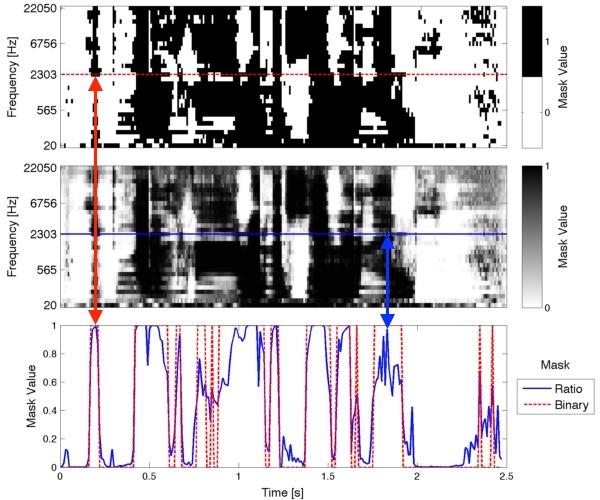
The binary mask is set to 1 when the target sound is louder than the unwanted sound(s), and 0 otherwise. The ratio mask is calculated as the ratio of target sound power to mixture sound power. From that definition, it should be clear that when the mixture consists of only the target sound, the ratio value will be 1. When the target is silent and there are some (or lots) of other sounds (making the mixture power large), the ratio value will be 0. When there is other sound that is at the same level as the target sound, the ratio value will be 0.5.
So does this ratio mask improve things? Judge for yourself below. But I think so.
Mixture
Binary mask (top panel, Fig. 1.)
Ratio mask (middle panel, Fig. 1.)
There are a bunch of other good reasons to prefer the ratio mask to the binary mask, too. For a start, if we measure how much unwanted signal is left in the outputs above, then we find that the ratio mask removes slightly more unwanted signal (the difference is slight, though).
Some reasons to prefer the ratio mask to the binary mask are conceptual, rather than practical. The proposal of the binary mask [2] was based, in part, upon the psychoacoustic principle of masking (see [3] for a review). Masking is when one sound renders another inaudible. Studying psychoacoustic masking reveals quite a lot about how the human auditory system works. In masking experiments subjects are generally played two sounds, with one usually varied in level, and asked whether one of the sounds is audible. In other words, the subject makes a binary decision (yes or no) about whether the sound was audible. However, if we were to repeat the experiment at a future date, or ask another subject the same question with the same sounds, we would not necessarily get the same answer. This is due to uncontrolled variables such as differences in the listeners' physiology, differences in their decision making processes, variations in external noise, etc. So instead of reporting the level at which the sound becomes inaudible, scientists tend to report the probability of audibility as a function of the level difference. This is known as a psychometric function. When the level difference is large, the probability of the sound being audible tends towards 0 or 1 (depending on which sound is louder). When the level difference is small, the probability tends towards 0.5. Note that this result is quite similar to that produced by the ratio mask. When described in this way, psychoacoustic masking is one application of signal detection theory. So describing psychoacoustic masking as "binary" doesn't really tell the whole story.
Some of Bregman's ideas about auditory scene analysis [4] (see previous post) are derived from gestalt psychology. One principle in particular is important in this context: the principle of exclusive allocation (often referred to as "disjoint allocation"). This is demonstrated below in Fig. 2. The basic idea is that sensory elements are generally attributed to one object or another. In the case of Fig. 2, the black–white edge is usually attributed to either the vase or the faces; the decision is binary.

The above example is from the visual domain, but there is some evidence that the same applies in the auditory domain [4]. However, this evidence is generally obtained from rather basic, and somewhat unrealistic, patterns of tones where some intermediate tones tend to cluster with one group of tones or another. Fig. 2 is similarly unrealistic because in practice the faces and the vase would have their own edges. If the objects overlap, the resulting edge would probably be assigned to the foreground object as it seems more plausible that the edge of the background object is occluded.
But what if sounds overlap? Generally speaking the aforementioned tone patterns are often too basic to suggest any kind of overlap of sensory elements; exclusive allocation seems reasonable. This phenomenon is not generally observed for more realistic stimuli such as speech [5]. This alternate mode of perception observed in speech is referred to as "duplex perception". Part of the reason for this difference in perception, perhaps, is summarised by Bregman [5]:
"Sound is transparent. A sound in the foreground does not 'occlude' a sound in the background in the same way as a visual object occludes our view of objects behind it."In the visual domain, objects are occluded because light emitted or reflected from the object does not reach your eyes. In the auditory domain, even if a sound source is visually occluded, its acoustic energy still usually arrives at the ears via numerous acoustic pathways (reflection, diffraction, etc.). Thereafter sounds are occluded by physiological, psychophysical, or psychological mechanisms, rather than the absence of an input. It therefore seems disadvantageous to make binary decisions for time–frequency units, which may contain information about multiple sound sources. A visual analogy is given in Fig. 3.
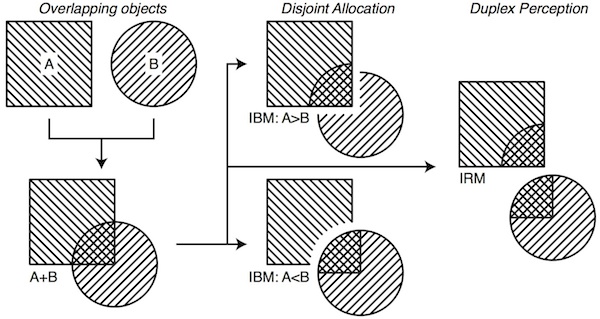
The two images on the left in Fig. 3 show two objects that are overlapped such that there is now a small common area. Using a disjoint allocation principle—demonstrated in the middle of the figure—the common area must be assigned to one object. The scenario is analogous to binary masking. The occluding object is corrupt whereas the occluded object is incomplete. Using a duplex perception principle—demonstrated in the right of the figure—the common area may be assigned to both objects. The scenario is analogous to ratio masking. The resulting objects are now complete, irrespective of the chosen source, although each is corrupted to some extent by the other. The ratio value indicates the extent of the corruption and hence how meaningful the area is likely to be to either source.
There are practical reasons to prefer a ratio mask over a binary mask too, since it gives greater improvement in speech intelligibility (e.g. [1]) and automatic speech recognition accuracy (e.g. [6]).
The main reason that the community is debating these two approaches is that whilst the benefits of a ratio mask are reasonably clear (not always, but most of the time), in practice it's very difficult to calculate the ratio value because we don't know anything about the sound sources. Binary masks are generally simpler to calculate. It seems the general feeling is that the advantages of the ratio mask are not worth the considerable extra effort required to calculate them. At the moment this may be true, but it's important that we don't let this stifle our ambition.
This blog post is adapted from a [hopefully] forthcoming book chapter:
C. Hummersone, T. Stokes, and T. Brookes, On the ideal ratio mask as the goal of computational auditory scene analysis. In: W. Wang and G. Naik (eds.) Advances in Modern Blind Source Separation Techniques: Theory and Applications. Springer, Berlin/Heidelberg (2013). (Subject to review.)
References
[4] Bregman, A.S.: Auditory Scene Analysis. MIT Press, Cambridge, MA (1990).
by Chris Hummersone
